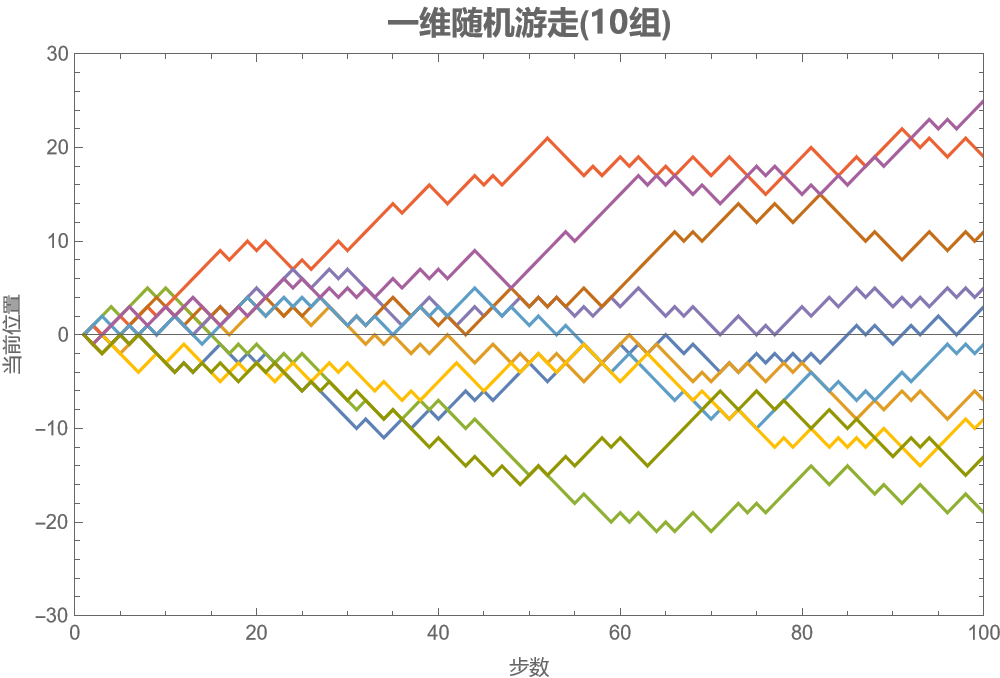
一维随机游走第n步时距原点的平均距离
一、定义 一个醉汉在一条笔直的公路随机游走,每一步都以 50% 的概率向前移动一步:\(+1\),或向后移动一步:\(-1\),即每一步都是一个独立的随机变量,记为 \(Z_{1},Z_{2},\dots\)。 设 \(S_{0}=0\),\(S_{n}=\sum\limits_{j=1}^{n}Z_{j}\),则级数 $ {S_{n}}$ 称为 \(\mathbb {Z}\) 上的简单随机游走。显然 \(-n\leqslant S_n \leqslant n\)。 在 \(n\) 步随机游走中,醉汉恰有 \(k\) 次向前移动的概率为 \(P_k:=P(\text{恰有}k\text{个}Z_i=1)=\dbinom{n}{k}\dfrac{1}{2^n}\),此时 \(S_n=2k-n\),所以一维随机游走中离原点的平均距离为: \[ E(|S_n|)=\dfrac{1}{2^n}\sum_{k=0}^n\dbinom{n}{k}\left|2k-n\right| \]