一、问题 已知一位小偷每次出手都以固定的概率 \(p_s\) 得手，并以固定的概率 \(p_a\) 被捕，且得手与被捕相互独立，问小偷在被捕前的平均得手次数是多少。 二、计算 2.1 问题重述 将原问题用数学语言重述。 首先，明确随机变量...

一、问题重述与求解 随机数：\(X_k\sim \mathbf{U}(0,1)\)。 n 个随机数之和恰能超过 1 的概率表达为数学语言为：\(P\{\sum_\limits{k=1}^nX_k>1 \bigcap \sum_\li...

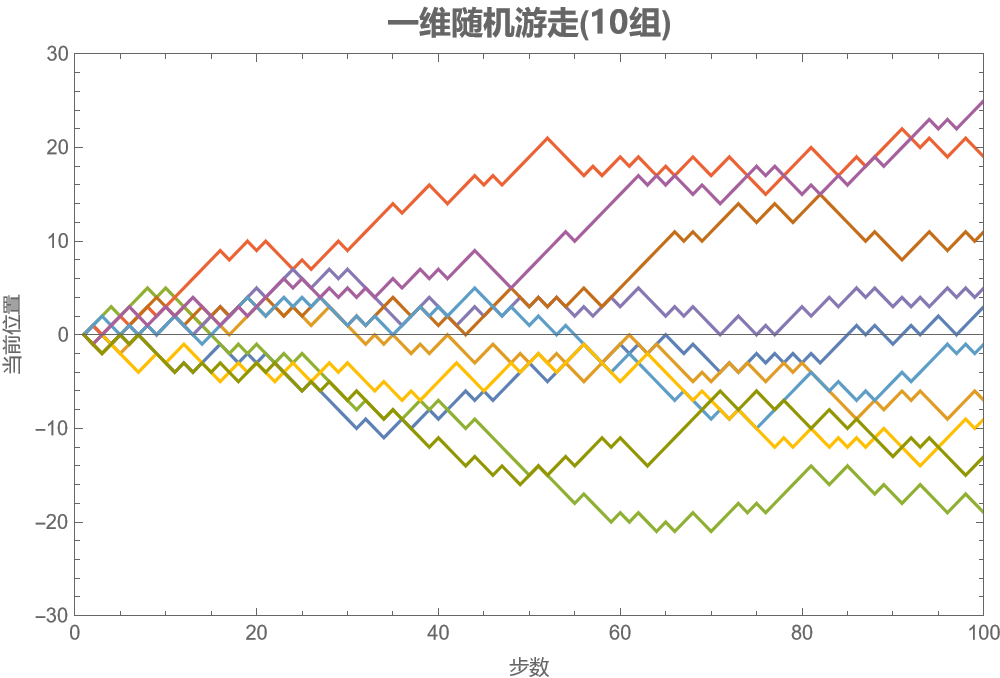
一、定义 一个醉汉在一条笔直的公路随机游走，每一步都以 50% 的概率向前移动一步：\(+1\)，或向后移动一步：\(-1\)，即每一步都是一个独立的随机变量，记为 \(Z_{1},Z_{2},\dots\)。 设 \(S_{0}=0\)，\(S_{n}=\sum\limits_{j=1}^{n}Z_{j}\)，则级数 $ {S_{n}}$ 称为 \(\mathbb {Z}\) 上的简单随机游走。显然 \(-n\leqslant S_n \leqslant n\)。 在 \(n\) 步随机游走中，醉汉恰有 \(k\) 次向前移动的概率为 \(P_k:=P(\text{恰有}k\text{个}Z_i=1)=\dbinom{n}{k}\dfrac{1}{2^n}\)，此时 \(S_n=2k-n\)，所以一维随机游走中离原点的平均距离为： \[ E(|S_n|)=\dfrac{1}{2^n}\sum_{k=0}^n\dbinom{n}{k}\left|2k-n\right| \]

一、问题 【题目】在自然数\(\{1,2,\cdots,N\}\)中随机抽取\(n\)个样本，求最小的\(k\)个样本的平均值的期望。 【定义】为方便讨论，记样本为\(\{X_1,X_2,\cdots,X_n\}\)，大小排在第\(k\)位的样本记为\(X_{(k)}\)。

一、问题介绍 1.1 背景 蒙提霍尔问题，亦称为蒙特霍问题或三门问题（英文：Monty Hall problem），是一个源自博弈论的数学游戏问题，大致出自美国的电视游戏节目Let’s Make a Deal。问题的名字来自该节目的主持人蒙蒂•霍尔。 详情参见：维基百科 1.2 玩法 1.2.1 原描述方式 背景：参赛者会看见三扇关闭的门，其中一扇门后面有奖品，选中后面有奖品的那扇门就可以赢得该奖品，而另外两扇门后面则没有任何东西。 当参赛者选定了一扇门，但未去开启它的时候，知道门后情形的节目主持人，会在剩下的两扇门中开启没有任何东西的一扇。主持人此时会问参赛者要不要换另一扇仍然关上的门。 问题：换另一扇门会否增加参赛者赢得汽车的机会率？